[toc]

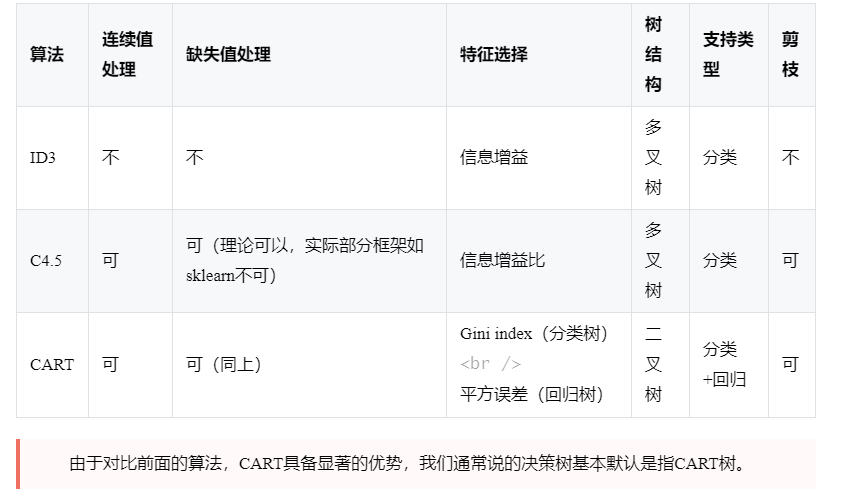
决策树基础

贪心决策树的案底

• 最基础的弱学习器——决策树，其贪心雅号来源于他的优化算法——贪心算法，也即每一步特征切分都是局部最优，而非全局最优。大抵就是只顾当前，不顾未来，之后咋样，我管不着的算法。

• 一些聊胜于无的专业术语：叶节点、根结点、内部结点。

  

• 贪心的决策树算法分为三个部分——如何切分（切分特征与切分点的选择）、决策树的生成、决策树的剪枝。

决策树切分

首先我们先从分类问题进行切入，回归问题将循序渐进的介绍，因为决策树最开始是专职处理分类问题，后随着要求的不断更迭，决策树算法也可以处理连续型与混合型。

不纯度

• 我们希望决策树的分支结点所包含的样本尽可能属于同⼀类别，即结点的 “纯度”（purity）越来越⾼。在分类树中，划分的优劣⽤不纯度度量（impurity-measure）定量分析。

  简单来说，不纯度就代表着不确定性，假如按照某种特征与切分点切分后，结果是将label五五分成，这也就代表了最混乱的状态，这类切分毫无意义，我奶奶来切都比他切得好。

• 分别为Entropy（熵）、Gini index（基尼系数）、Classification error（误分类误差）。以下的p均代表label占总体的比例，$p_1$代表第一类label的占比。

• Entropy

  $$Entropy(p) = -\sum_{i=1}p_i*\log_2p_i$$

  当切分的子节点为2个时，易得该项为Cross-Entropy。另外值得一提的是，信息熵本身是一种主观发明，是一种定义，而非对事物规律的发现，包括以2为底是为了适应二进制，实际可以是大于1的任何数，都符合单调性。

• Gini index

  $$Gini(p) = 1 -\sum_{i=1}p^2_i$$

• Classification Error

  $$CE(p) = 1-\max(p)$$

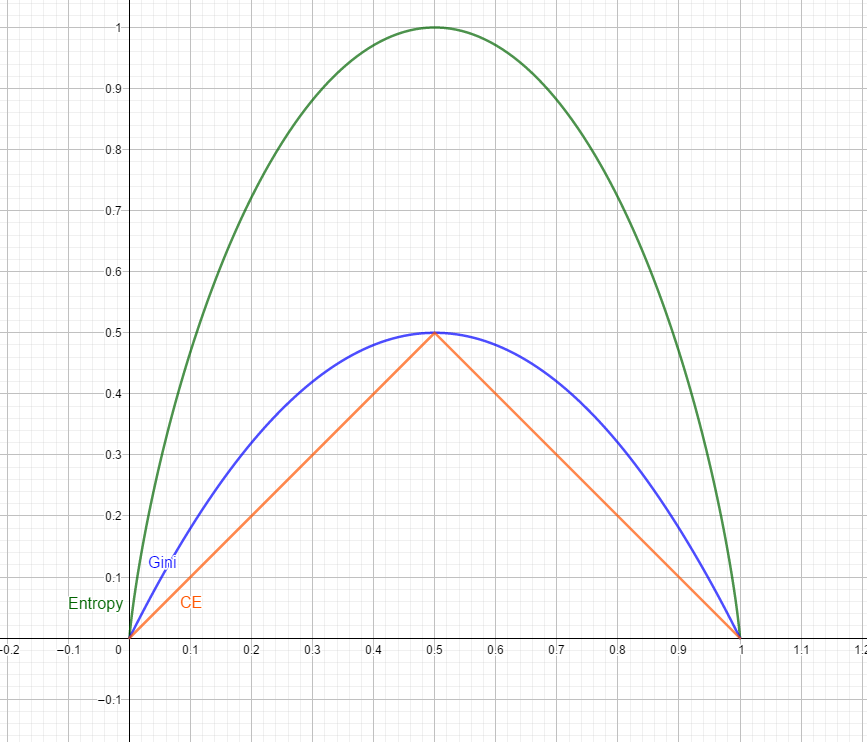
• 决策树最终的优化⽬标是让叶结点的总不纯度最低，即对应衡量不纯度的指标最低(但实际上贪心算法是短视的,它只能保证每一步的总不纯度是最小的,无法倒退)

信息增益

• 通常我们说的信息增益，是默认信息熵作为不纯度的度量。

• 定义信息增益为Gain, 父结点不纯度impurity为I(parent),子结点的总不纯度为I(child)，故：

$$Gain = I(parent) - I(child)$$

• 由于I(parent)是既定的，故要使得Gain最大，实际上是需要I(child)最小，对于I(child)，其实际为条件不纯度的加权平均综合。

• 若以熵为不纯度，则I(child)等价于条件熵。设$H(Y|X)$代表条件熵，X表示某个具体的特征，x则表示该特征中某个具体的分类，$H(Y|X=x)$代表后验熵（注意负号），那么可知信息增益优化的目标就是让条件熵最小。

  $$H(Y|X) = \sum_{x\in X}p(x)H(Y|X=x)\\$$ $$H(Y|X=x) = -\sum_{y\in Y}p(y|x)*\log_2{p(y|x)}$$

决策树生成（早先的两种算法）

ID3算法——树之明灯

撒旦来了都说好的ID3算法原型来源于 J.R Quinlan 的博士论⽂，是早期基础理论较为完善，使用较为⼴泛的决策树模型，在此基础上 J.R Quinlan 进行优化后，陆续推出了C4.5 和 C5.0 决策树算法。

ID3算法的核心是在决策树各个结点应⽤信息增益准则选择特征，递归地构建决策树。具体⽅法是：

1. 从根结点开始，对结点计算所有可能的特征的信息增益。

2. 选择信息增益最大的特征作为切分结点的特征。

3. 由该特征的不同取值建立子结点 再对每个子结点也递归的使用如根节点同样的处理方式。
4. 直到所有特征的信息增益都小于设定的阈值（再切分的收益很小了）或没有特征可以选择为止（信息增益已经没有压榨空间了），最后得到一颗决策树。

ID3算法的优缺点

Advantages: 开创性，他的到来为后来的各种进阶算法打下了基础。

Disadvantages（包揽了能想到的所有缺点）:

• 不能处理连续型数据。

• 信息熵为基础的信息增益，如同一个鼓动多分类的罪犯，他的滔天大罪就是倡导毫无必要的多分类。因为分类个数越多，信息增益就会变高，于是乎讨喜的特征总会是那些让人直呼上帝的多分类特征。极端条件下，每个样本对应一个分类的特征占据了信息增益最大化的最优解，而这不是我们想看到的。

• 无法很好的处理缺失值。

• 没有任何的剪枝处理，严重过拟合。

• ID3如此之多的缺点，堪称经典负面教材，它赤裸裸的展示了其堪称完美的体无完肤，为后来的C4.5、C5.0等算法开创了鲜明的道路，值得谬赞。

附一个ID3的代码（仅供参考）：

def calEnt(dataSet):
    n = dataSet.shape[0] # 数据集总⾏数
    iset = dataSet.iloc[:,-1].value_counts() # 标签的所有类别
    p = iset/n # 每⼀类标签所占⽐
    ent = (-p*np.log2(p)).sum() # 计算信息熵
    return ent

# 创建数据集
import numpy as np
import pandas as pd
def createDataSet():
    row_data = {'accompany':[1,1,1,0,0],
                'game':[1,1,0,1,1],
                'bad boy':['yes','yes','no','no','no']}
    dataSet = pd.DataFrame(row_data)
    return dataSet
dataSet = createDataSet()

"""
参数说明：
 dataSet：原始数据集
返回：
 axis：数据集最佳切分列的索引
"""

# 选择最优的列进⾏切分
def bestSplit(dataSet):
    baseEnt = calEnt(dataSet) # 计算原始熵
    bestGain = 0 # 初始化信息增益
    axis = -1 # 初始化最佳切分列，
标签列
for i in range(dataSet.shape[1]-1): # 对特征的每⼀列进⾏
    循环
    levels= dataSet.iloc[:,i].value_counts().index # 提取出当前列的所有
    取值
    ents = 0 # 初始化⼦节点的信息
    熵
    for j in levels: # 对当前列的每⼀个取值进⾏循环
        childSet = dataSet[dataSet.iloc[:,i]==j] # 某⼀个⼦节点的dataframe
        ent = calEnt(childSet) # 计算某⼀个⼦节点的信息熵
        ents += (childSet.shape[0]/dataSet.shape[0])*ent # 计算当前列的信息熵
        print(f'第{i}列的信息熵为{ents}')
        infoGain = baseEnt-ents # 计算当前列的信息增益
        print(f'第{i}列的信息增益为{infoGain}')
        if (infoGain > bestGain):
            bestGain = infoGain # 选择最⼤信息增益
            axis = i # 最⼤信息增益所在列
            的索引
            return axis
        
# bestSplit(dataSet) # 返回的结果为0，即选择第0列来切分数据集


"""
函数功能：按照给定的列划分数据集
参数说明：
 dataSet：原始数据集
 axis：指定的列索引
 value：指定的属性值
返回：
 redataSet：按照指定列索引和属性值切分后的数据集
"""
def mySplit(dataSet,axis,value):
    col = dataSet.columns[axis]
    redataSet = dataSet.loc[dataSet[col]==value,:].drop(col,axis=1)
    return redataSet



"""
函数功能：基于最⼤信息增益切分数据集，递归构建决策树
参数说明：
 dataSet：原始数据集(最有⼀列是标签)
返回：
 myTree：字典形式的树
"""
def createTree(dataSet):
    featlist = list(dataSet.columns) # 提取出数据集所有的列
    classlist = dataSet.iloc[:,-1].value_counts() # 获取最后⼀列类标签
    # 判断最多标签数⽬是否等于数据集⾏数，或者数据集是否只有⼀列
    if classlist[0]==dataSet.shape[0] or dataSet.shape[1] == 1:
        return classlist.index[0] # 如果是，返回类标签
    axis = bestSplit(dataSet) # 确定出当前最佳切分列的索引
    bestfeat = featlist[axis] # 获取该索引对应的特征
    myTree = {bestfeat:{}} # 采⽤字典嵌套的⽅式存储树信息
    del featlist[axis] # 删除当前特征
    valuelist = set(dataSet.iloc[:,axis]) # 提取最佳切分列所有属性值
    for value in valuelist: # 对每⼀个属性值递归建
        树
        myTree[bestfeat][value] = createTree(mySplit(dataSet,axis,value))
        return myTree
    
myTree = createTree(dataSet)
myTree

C4.5算法——优秀的乌龟

C4.5算法改用信息增益比最大化来切分叶节点。

• 对于D数据集的a特征，Gain_Ratio(D,a)为信息增益比,Gain(D,a)为信息增益,IV(a)为该特征的信息熵,p(i)为i特征分类的样本占比。

$$Gain\_Ratio(D,a) = \frac{Gain(D,a)}{IV(a)}$$ $$IV(a) = -\sum_{i\in{a}}p(i)\log_2p(i)$$

• IV(a)作为该特征的固有值(intrinsic value)。当a的取值i越多时，IV越大。并从总体而言，增益率准则会分类较少的特征有所偏好。
• 启发式的应用——该算法不是将所有特征的信息增益比计算出来直接比大小，而是先算出信息增益，再根据信息增益的大小，选出几个信息增益靠前的，再计算其中信息增益比最高的。

C4.5算法中加入了连续变量的处理

• 如果输入的特征是连续型变量，判定完毕后，将其按照升序排列，并从相邻2个数之间选取平均值作为切分备选点。N个值就有N-1个切分点，每个切分点都代表一种切分的可能性，也即将N个数字进行N-1种2分，并将两个连续值域对应成两个离散的类别。假设连续特征里有一万个大小不等的数，那就有9999中切分方法，显然这带来的就是一个让人心脏骤停的后果 —— 慢！

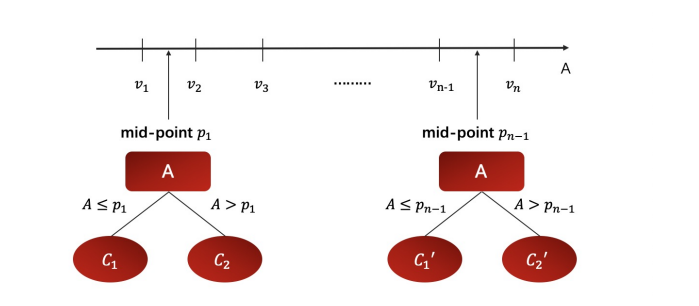
C4.5算法的优缺点

Advantages:

• 可处理连续型
• 提供了启发式
• 可用于分箱
• 不会像ID3那样，鼓励多分类，Gain Ratio对多分类趋势进行了打击。
• 可以处理缺失值了，将缺失值当做一种特殊的分类处理。

Disadvantages:

• 慢！

• 过拟合呢？哦！弟中弟啊，怎么还不解决那该死的过拟合！

• 另外可以稍加延伸的是，多分类特征编码的问题也没有解决，Onehot的维度灾难问题悬而未决。

• 回归问题怎么办？只能做分类问题吗？我堂堂决策树！难道！就不能解决回归问题吗！你说啊！

决策树的剪枝

预剪枝与后剪枝

众所周知，当假设空间中有不同复杂度的模型时，基于奥卡姆剃刀——如无必要、勿增实体的原则，我们通常会选简单的模型。

那么对于一颗力求简洁的树而言，枝繁叶茂就是它的头等大罪，故树深(max_depth)与叶子数(num_leafs)两个参数是优化的目标。高则过拟合，低则欠拟合，我们通常会想取乎其中，但对于决策树问题，它不加限制，往往只会是过拟合，所以我们需要限制它的生长。

常⻅的剪枝策略有 ”预剪枝“（Pre-Pruning）和 ”后剪枝“（Post-Pruning）

• 预剪枝：如果当前结点的划分不能带来决策树泛化性能(分类问题通常是：Accuracy)的提升，则停止划分。

• 后剪枝：先生成完整的树，然后从下到上对非叶节点进行考察，如果将该结点对应的子树剪枝为一个叶节点能带来泛化能力提升，则替换。

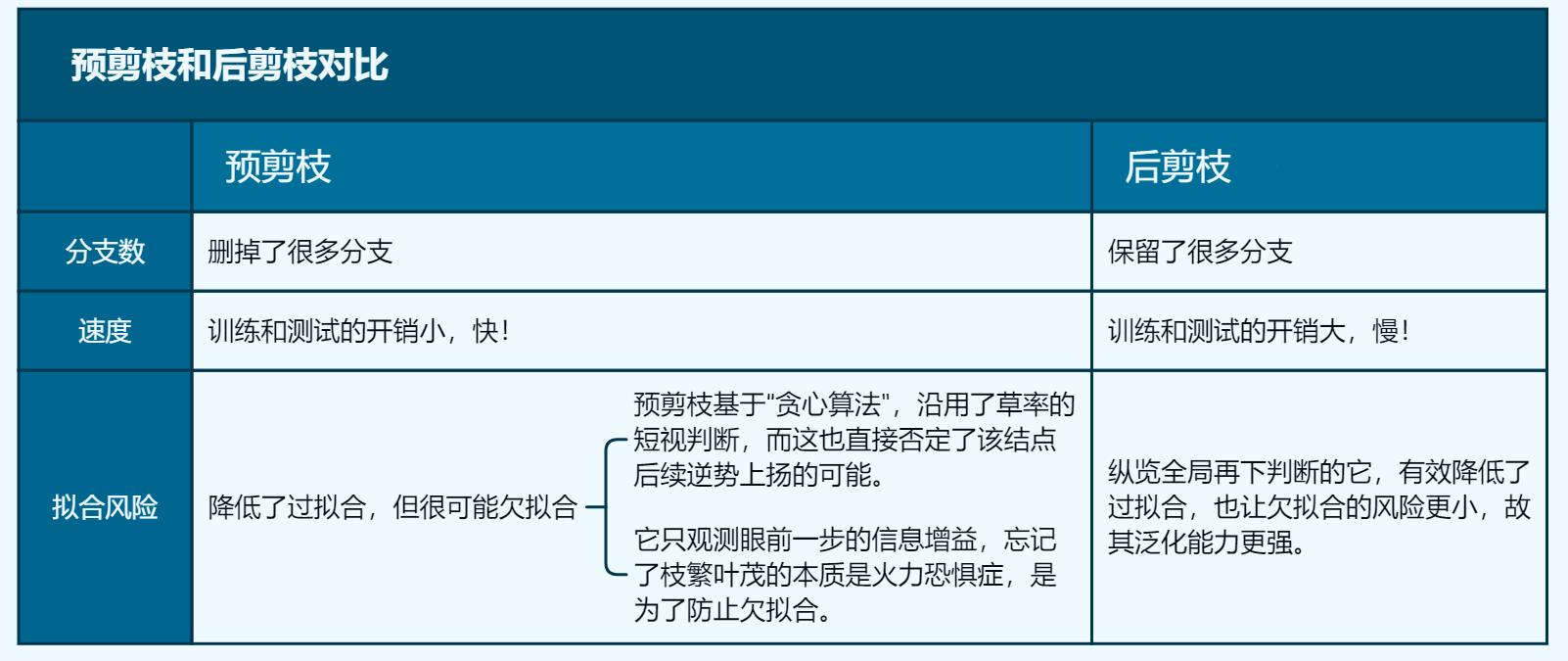
随着以上的剪枝思想的考量，应运而生的是极为重要的基学习器——CART算法

CART算法——臭皮匠

主要变化：

• 二叉树，没有该死的多叉树了！二叉树原则：条件成立向左，反之向右。
• Label可以是离散型，也可以是连续型，终于可以解决回归问题了！
• 连续型数据不需要离散化，C4.5算法那个乌龟一样慢的分箱思路终于宣告结束。

---

CART分类树：

• Gini准则，也即用gini系数平换信息增益中的信息熵（不纯度的度量变换）。
• 对于分类问题，基于子节点的加权平均错误率与父节点的比烂，一轮开摆后，如果行情见长，就断子绝孙。

CART回归树：

• 平方误差最小化准则，先遍历特征j，找到切分点s。在此特征此切分的情况下，计算一个平方误差最小值，并记录下来。设某个连续特征有n个数，则该特征需要正常需要计算(n-1)次，诶？这不是又成乌龟了！

• 这种划分问题被称之为NP难问题，实际的优化具备启发式，总之是可以更快！但在这里不展开了。

• 以下为优化目标解析式, 其中C1为左子树，C2为右子树, yi为要搜寻的最优y值，其实就是切分后子树的y样本均值（算术平均值就是优化的数学期望）：

  $$\min_{j,s}[\min_{c1}\sum_{x_i\in{R_1(j,s)}}(y_i-c_1)^2+\min_{c2}\sum_{x_i\in{R_2(j,s)}}(y_i-c_1)^2]$$

• 其实扯那么多也就是看所有特征的所有切分，哪个能让（左子树离差平方和+右子树离差平方和）最小。唯才是举！你有货你就来！

• 具体的方法是MLE(极大似然估计)+梯度提升的方法来找到最优值。（这里就不展开啦，大家肯定都懂）

决策树及三大基本算法小结

决策树优点

1. 白盒模型，有解释性，因为树可以画出来，不像云山雾绕的神经网络。
2. 树模型只管相对大小，不需要搞花里胡哨（归一化、标准化）
3. 缺失值也可以不管！统一看做一个特殊类（比所有数都小的数）。
4. 可以同时处理数值型和分类型。

5. 预测时的计算成本相比其他的算法要低，为训练样本数的对数$\log{n}$。

6. 可以处理多输出问题，也就是不止一个label，预测对象可以是一个label矩阵。

7. 可以使⽤统计测试验证模型，这让我们可以考虑模型的可靠性。

决策树缺点

1. 过拟合——方差太大。
2. 欠拟合——存在偏差，究其根本就是不稳定性，数据集很小的变化可能会导致生成一个截然不同的树。
3. 贪婪算法，优化目标仅局部而非全局。
4. 部分领域不擅长，例如XOR，奇偶校验或多路复⽤器问题
5. 如果标签中的某些类占主导地位，会创建偏向主导类的树——数据样本不平衡时，该算法听风是雨，人云亦云。
6. 决策树是非参数模型,我们并无法通过决策树得知任何关于分布的参数。
7. 对超多分类的特征比如邮编、地区等依然束手无策，onehot？10000个分类的单特征，用one-hot+PCA降维同样折磨，维度灾难不说，哪怕去掉count == 1的部分剩下的依然让人哀嚎，算到天荒地老。但如果离散编码，那就是默认它们之间的大小关系，编码数字大就代表更大这种错误的信息，愚蠢的CART树如何识得此阵？只能强行搞一波地域黑，用邮政编码的大小给每个地区安排上了。而为了强行能够使用，我们必须要先对这种变量聚类分箱处理，这一顿操作下来，如此的折腾，两眼一黑的我不禁想问，这该死的决策树为什么不考虑到这一点呢？我只想安静的调包，诸君想必也是吧。

小结

• 虽然说存在剪枝的操作可以一定程度上限制过拟合，但实际决策树仍然是一个极度过拟合的算法。我们需要一些其他的方式来防止过拟合。

• 单颗决策树如此的不稳定，多颗树集成学习的犯罪动机初见端倪。

• 基于决策树算法，后续引入的四大集成思路也慢慢浮出水面——Bagging、Boosting、Stacking、Blending。而这些也是现在工业界炙手可热的集成算法框架，尤其是Boosting算法。

Bagging

CART决策树白天打死打生，疯狂运算，夜里脱去一身的疲惫，常常孤枕难眠，深感独木难支。“我们联合”与“三根破树枝顶根紫檀木”的口号也在脑海中声势渐大。它意识到这可能是它此生绝无仅有的机会，自己的不稳定性就在于老是独断专行，而且很容易听信谗言，周围数据对他的影响太大，一粒老鼠屎总能坏了一锅汤。虽然它确信自己是在优化的路上，但是这种伴随极大不确定性的震荡上升（方差）令他深恶痛绝，于是他垂死病中惊坐起！决定！Bagging起来！

• Bagging的核心一言以蔽之：并行与重复采样，天下兴亡匹夫有责，分则能成！

• Bagging存在对袋外数据(out of bags)的利用，也就是藏了一手数据，用来防止过拟合，类似于交叉验证的思想来选择训练集。

• Bagging用来筛选数据的方法是重复放回采样，采样次数通常就是数据集样本个数次，假设有n个样本，那么采样的比例（每个样本被抽中的概率）可以计算如下：

  $$\lim\limits_{n\to+\infty}(1-(1-\frac{1}{n})^n) = 1-\frac{1}{e}\approx0.632$$

随机采样(Bootstrap Sampling)：从n个样本里重复有放回的采样n次，然后重复采样的部分删去。

• Bagging是并行式集成学习的著名代表，每进行一次Bootstrap Sampling，都会生成不一样的采样集。假设基学习器为决策树，那么对每个采样集，都会生成一颗决策树（我的兄弟来辣）。

  • 对分类任务，使用Voting（投票法），实际预测结果为所有决策树的众数。
  • 对回归任务，使用Model-Averaging(平均法)，实际预测结果为所有决策树的平均数。

Bagging基本思想小结

1. 给定一个弱学习器和一个训练集
2. 弱学习器要弱，不能太准。
3. 将该学习算法使用多次, 再进行投票or平均。
4. 最后结果准确率将得到提高。
5. Bagging通过降低基分类器的方差，改善了泛化误差。如果基分类器不稳定，bagging有助于降低训练数据的随机波动导致的误差。
6. 基学习器们和样本们给我听好了！我Bagging算法只办三件事！公平，公平，还是TM的公平！每个样本被选中的概率与权重都相同！每个基学习器的投票权重也相同！（Boosting：我怀疑你在内涵我）
7. 并行！每个基学习器都是同时开始的（当然实际上不是，没有那么多线程），且之间互不影响，各扫门前雪，然后投票就完事儿啦。（这当真好吗？）

RandomForest——Bagging手下头号大将（基本就一个）

1995年，某个伟大的人出生了，伴随着他的诞生，由Leo Breiman和Adele Cutler提出的RandomForest与有荣焉，一并到来。

Random

随机森林的核心是随机，其随机体现在三个方面：

1. 行随机：Bagging头号唯粉——每颗决策树的采样集随机。
2. 列随机：弱水三千，仅取两千——通过设置超参数，可调节特征选择的比例，也即每颗决策树的列也各有不同。
3. 切分随机：偶尔随性，超越贪婪——对于每颗子树（通常都是CART），不一定选择最优的切分特征来切分，而是在排名靠前的几个特征里按照一定权重来选择，大部分时候选最优，偶尔选次优的特征来切分，以此脱出贪婪算法的牢笼，以求寻找到全局最优的切分可能（当然大概率更差），别问全局最优怎么来的，妙手偶得之！

Forest

所谓森林也就是指随机森林是由多颗决策树组成的森林，最后的预测结果是所有树的联合表决。回归则平均、分类则众数。

随机森林优缺点

Advantages:

• 随机森林在运算量没有显著提高的前提下提高了预测精度。
• 有效降低了过拟合，也即降低了泛化误差中的方差部分，只要树足够多（数也足够多），再大的方差都能给你平下来。
• 在sklearn中，可以借助API来观察特征重要性，谁在摆烂一览无余，然后大搞末位淘汰的资本主义。
• 更好的应对了无用特征，因为随机，总有它不在的时候。
• 更好的应对了异常值，因为随机，总有它不在的时候。

Disadvantages:

• 森林中的决策树个数很多时，训练需要的时间和空间会较大。

• 降低了方差，但没有更好的处理偏差。

• 相比于单一决策树，它的随机性让我们难以对模型进行解释。但实际决策树本身也很随机，其实这也不算缺点。

• 不擅长回归问题，这也是CART的老毛病了，没办法，子承父业。

Boosting

Boosting思想起源

Boosting思想起源于PAC（Probably Approximately Correct）学习模型。当时是1989年有两个人(Kearns 和 Valiant) 认为学习器生而平等，提出了猜想——弱学习器和强学习器学习能力等价，一年之后，Schapire通过多项式算法证实了前人的猜想，并正式提出了Boosting算法，但是这个刚具雏形的版本还不能应用于实际。

AdaBoost——万恶之源

1997年，风云激荡，那年我两岁，同年，Schapire提出了AdaBoost（Adaptive Boosting——自适应增强算法）。

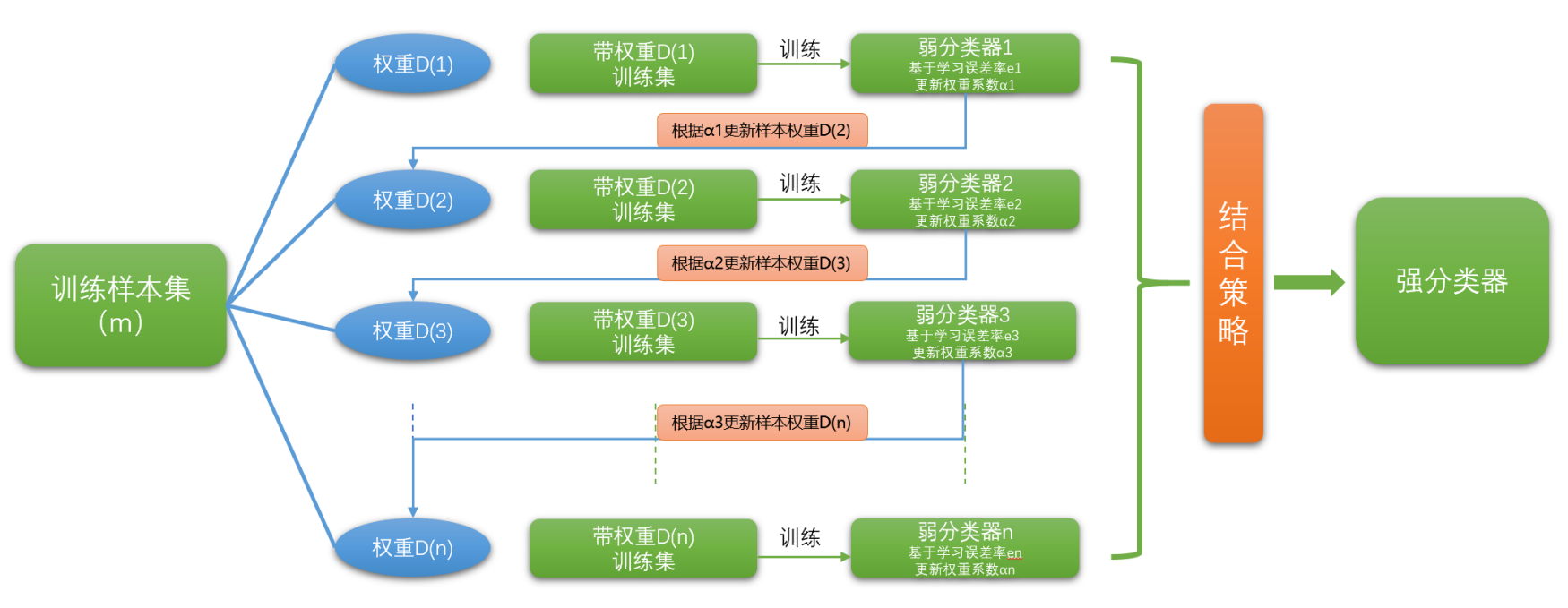
简要概括，Boosting算法的核心思路大致为：串行与权重调整，前人栽树，后人乘凉，对症下药，级联提升。成不在我，功不唐捐。

抽取方式：不放回抽取，子集等于全集，每个采样集内样本完全一致。

算法步骤简述：

1. 初始化训练数据的权重。假设有N个样本，则每个样本的权重统一为 1/N。

2. 训练弱学习器。

3. 专注错题！调整样本权重，根据训练结果将预测错的样本的权重提高，具体为二分之一法则，预测错的样本权重和为1/2，预测正确的样本权重和也为1/2，一般而言，我们要求弱学习器的预测准确率下界至少要为50%，这样的分配也会使得错误样本的权重高于正确样本。

4. 资源倾斜！调整弱学习器的权重，早期的Adaboost只能进行分类问题，这里以分类问题举例，假设某个弱分类器错误率为e，它的权重为α：

   $$\alpha_k = \frac{1}{2}\ln\frac{1-e_k}{e_k},0\le e_k \le 1$$

   也即，当错误率 e 越高，该分类器的权重 α 越低。

推导公式传送门：集成学习之Adaboost算法原理小结

1. 对于分类问题，每个弱学习器的学习错误率是样本错误率的加权平均（样本权重不一），根据学习错误率，每个弱学习器都有一个对应的学习器权重，最终的强学习器（整个AdaBoost）的结果也将加权计算得出。

   对于回归问题，计算样本的相对误差有三种方式，具体可以参照上面的大佬传送门中，有详细信息。最终的强学习器采用的是加权中位数，而非平均。

对于基学习器的选择的考虑

选择基学习器值得考虑的两种论调：

可以用强学习器（铁血抱团詹…咳，强强联合派）

• 实际中什么模型都可以集成，但是弱分类器的训练运行成本比较低罢了。（那显然是你的硬件不行！你在无理取闹！你的俱乐部有工资帽！不是我球员不行，不是我的算法不行 okay？）
• 哪怕是强学习器也有异质性，只是…..不是那么的不一样罢了！那能叫一样吗，那叫英雄相惜，我当初也是弱学习器来的，你个弱学习器初来乍到，那么幼稚的分类你都能提出来，你也不看看你的准确率和AUC，你懂个屁！

不建议用强学习器（弱分类器是为团队而生的，以弱胜强派）

• 如果采用强分类器，每个分类器都可以很好的描述这批数据，分类器就会趋同，这样集成就没有意义了。因为弱，所以头脑风暴的基点很初级，为看似幼稚、前途未卜的一意孤行存续了可能，谁也不知道这帮无知的家伙能去往何方，但它们的勇敢在决策者的信任下得到发挥，也偶尔能逼近更好的真相，从而降低偏差(bias)。
• 集成学习希望的就是每个分类器的差异越大越好，这样每个分类器都能表述关于数据的一些不同的信息，然后通过集成，得到一个好的分类结果。
• No free lunch：若每种问题出现的概率是均等的，每个模型用于解决所有问题时，其平均意义上的性能是一样的。而如此一来，弱学习器的低成本就具备优势了。

机器学习的目标不是放之四海而皆准的通用模型，而是关于特定问题有针对性的解决方案。

Occam’s Razor：如无必要，勿增实体。俄罗斯方块中最能适配的方块往往是结构单一的1x4长条。

一般而言，我们会选择弱学习器作为基学习器，而在最后的模型融合时，考虑更高阶的强强联合，也即Voting、Stacking、Blending。

AdaBoost的优缺点

优点：

• 有效降低了偏差
• 可以整合不同的分类算法作为基分类器
• 很好的利用了串联（级联）思路
• 不用担心over-fitting（这个是较难理解的，需要对Margin理论和加性模型的本质进行深挖）

缺点：

• 原初算法无法进行回归处理（已改良）
• 分类问题需要将Y编码为-1，+1。
• 弱分类器的数目需要超参优化
• 异常样本在迭代中可能会获得较高的权重（总算不明白还要硬算，认为是自己的问题而不是样本的问题）
• 数据不平衡问题束手无策
• 慢！——玛德怎么老是慢啊？（这一个字相当折磨，慢导致了它几乎无法被优先考虑，改变也势在必行，Lightgbm表示自己已经按捺不住表现欲了——被狠狠按下，xgboost在旁边点了根烟，半天说不出一句话）

​

小结

AdaBoost作为Boosting中第一款具备实操价值的算法，它所采用的思路和沿袭Bagging的RandomForest大相径庭。RandomForest，侧重优化方差；AdaBoost，侧重优化偏差。

---

RF（随机森林简写）平等的看待了所有的样本和所有的基学习器，而实际上，每个样本和每个学习器对实际目标的贡献其实是不相等的，变好变坏没有奖惩，没有区分，似乎有了些理想乡的味道，可我们的算法归根结底是目标导向的。

或许真正目标导向的平等应该在不同的维度上实现不一的加权平均，或许在更高的非线性上，在更严谨而不可抵达但可以持续逼近的复杂与规约之中，在无限收紧的泛化上界里。但无论如何——绝对的算术平均肯定不是最优的。当然这也并非是毫无收获的，voting关门开窗，切实降低了方差，也确实限制了过拟合。

---

AdaBoost 基于Boosting，站在侏儒的肩膀上试图眺望，慢慢的侏儒也并非侏儒，它似乎已经成了后辈的巨人。巨人之所以是巨人，因为他得到了权重的认可。而他成为巨人的方式，也是对不同样本的区别处理以及对前辈经验的承袭。

然而，这样的传承或许是要付出代价的，祖宗不足法，人言不足畏，有了前辈的指示，也有了前辈的限制。缩小偏差的代价也渐渐凸显——较大的方差。

我个人认为，Boosting算法是要更加有价值的，它让每个基学习器之间的相互作用发挥了价值，而非是Bagging这般各自为阵，在最后关头再融合决策。这其实是非常低效的，这种独立性和随机性当然保证了低方差，但是放弃合作的机会成本是否过大了呢？

---

举个例子，就好比两支不同的部队执行任务，RandomForest部队选择让所有士兵同时出发（并行），每个士兵都发挥主观能动性，给予他们随机的配备与信息。由于初始信息的不同，部队里有些士兵发现了更好的道路与方案，他们按图索骥，找到很好的完成任务的方式。虽然所有士兵的执行逻辑完全一致，有的士兵则运气没那么好了。最后指挥部，会依照士兵们的执行情况（训练），选择下一个执行类似任务的方式（预测），而指挥部选择的竟然是他们所有选择的折中方案。且在任务过程中，士兵之间没有任何的交流，指挥部也没有侧重听取那些找到好方法的士兵，也没有针对性的对某个几乎所有士兵都认为那是个大坑的特定路径予以更多的观照（平等对待错误样本）。这样大开大合的“公平方案”当真是我们需要的吗？

AdaBoost部队似乎又走向了另外一个极端，他让士兵一个一个出发（串行），并且每个士兵都给予了相同的信息。因为每个士兵最开始接受的训练内容一致（数据集都为全集），他们的执行逻辑也极为相似，这的确有可能使得他们会犯同样的错误。但是由于士兵是一个一个出发，前者完成任务之后会给后者通风报信，让后者必须注意他曾经踩过的坑，并坚定的信任这些信息且关注它们，当然这可能是个好主意，也可能不是。每个士兵都按照这样的方式逐次完成任务，绝对的参考了前者的信息，并完整传达了信息给后者。随着最后一名士兵汇报完毕，指挥官开始认真的审视所有士兵的完成情况，并且给他们的成绩进行一个评分，而评分的标准是按照他们的上一个士兵所提供的信息来做参考的。最终按照他们的评分，加权平均得到一个执行方案，而这个执行方案将作为对未来类似任务的战备方针。这听起来好像更加的科学，但是事实真的如此吗？

就我个人拙见与测试结果而言，仅从adaboost和randomforest上看，后者的性能绝大部分情况下更好，而且其运算速度上来说也更加快速。这是否意味着其实Bagging这个看似反直觉的方案反而是更合理的？那如果我们要优化Boosting算法，如何在不更改基学习器（比如CART树）的前提下，通过单纯的优化策略，使得Boosting达到理想的性能呢？

且实际操作过程中，我们惊人的发现AdaBoost并没有显著的过拟合现象，这到底是什么原因呢？虽然未来的Boosting算法中不乏有惊世骇俗之辈，但他们或多或少的融入了其他的思想和优化目标，而AdaBoost作为古早的算法也能够有着不俗的对抗过拟合的特性，这到底是为什么呢？

AdaBoost的理论升级之路

RandomForest在此拿来和AdaBoost来较量，也在于在这段时光中，两个算法的提出者也在过程中进行过对抗学习。

关于为何AdaBoost算法能够很好的对抗过拟合，随机森林的二位创始人之一——Leo Breiman曾经为AdaBoost的泛化界提出过一个重要假设，加速了该算法的优化历程。西瓜书的作者周志华教授以及南京大学的高尉教授也为此算法做出了突破贡献——让泛化误差上界更加收紧。

那么“Boosting Margin”到底是什么？

而这一部分要说起来，就会稍微有些晦涩了。我也要努力学习搬砖，挖个坑之后填。